1 Aufgabenanalyse

1.1 Zusammenfassung

Es soll die Dimension einer Matrix eingelesen werden. Zudem kann es auch Sperrfelder geben, die in der Matrix markiert werden. Vom eingegebenen Startpunkt aus, soll eine zusammenhängende Folge von Rösselsprüngen ausgeführt werden, so dass jedes freie Feld genau einmal besucht wird.

Am Ende soll die Matrix mit einer möglichen Sprungfolge ausgegeben werden (wenn es sie gibt).

1.2 Auflösung in strukturelle Bestandteile

Die Aufgabe wird nach dem EVA – Prinzip (Eingabe – Verarbeitung – Ausgabe) strukturiert. Dies findet sich auch in den Modulen wieder.

1.2.1 Eingabe

Daten die einzugeben sind:

Dimension in m – Richtung (Zeile)
Dimension in n – Richtung (Spalte)
Startpunkt (mit m, n – Koordinaten)
Anzahl der gesperrten Felder
Gesperrte Felder (mit m, n – Koordinaten)

Diese Daten werden aus einer Eingabedatei ausgelesen und in einer entsprechenden Datenstruktur abgelegt. Dabei kann auch Kommentar in der Eingabedatei stehen. Dieser wird mit ’**’ eingeleitet und gilt für die restliche Zeile (Zeilenendkommentar).

Zum Format der Eingabe:

Pflichteingaben:

1. Zeile: zwei Ganzzahlen im Bereich [1,6] [1,6] - Dimensionsangaben

2. Zeile: zwei Ganzzahlen im Bereich [1,m] [1,n] – Koordinaten des Startpunktes

Erweiterte Eingaben:

3. Zeile: Ganzzahl im Bereich [0,m·n-1] – Anzahl Sperrfelder

folgende Zeilen: zwei Ganzzahlen im Bereich [1,m] [1,n] – Koordinaten des Sperrfeldes

Als Fehler werden die Eingaben behandelt, die nicht den oben genannten Restriktionen unterliegen.

Zudem wird es als falsch angesehen, wenn am Zeilen- wie auch Dateiende hinter den Daten noch Zeichen folgen, die kein Kommentar sind. Leerzeilen sind aber überall in der Datei möglich.

1.2.2 Verarbeitung

In dem Modul Verarbeitung befindet sich der Hauptalgorithmus, der eine Folge von Rösselsprüngen ermittelt.

Vom angegebenen Startpunkt aus werden Sprünge auf freie (kein Sperrfeld oder noch nicht besuchte) Felder ausgeführt. Ziel ist es mit einer durchgehenden Folge von Sprüngen alle Felder, die keine Sperrfelder sind, genau ein Mal zu besuchen.

Für den Ausgang gibt es mehrere Möglichkeiten. Es kann keine, eine oder mehrere Lösungen geben, wobei bei mehreren Lösungen nur die erste gefundene Lösung ausgegeben wird.

Bei der Ausführung des Algorithmus wird die mögliche Sprungfolge in der Matrix gespeichert.

1.2.3 Ausgabe

Die Ausgabe gliedert sich in zwei Bereiche, die Ausgabe der Ergebnisse und die Fehlerausgabe, die sämtliche Fehler aus Eingabe und Verarbeitung verarbeitet.

Die Ausgabe der beiden Bereiche erfolgt in eine Ausgabedatei mit der Endung ".out". Dies kann nicht möglich sein, wenn falsche Programmparameter angegeben wurden oder wenn die Ausgabedatei schon existiert. Dann werden die Daten direkt auf dem Bildschirm ausgegeben. Um einfacher Testen zu können, erfolgt die Fehlerausgabe mit dem Programmparameter “-debug“ zusätzlich auf dem Bildschirm. Außerdem wird eine bestehende Ausgabedatei mit dem Parameter “-overwrite“ überschrieben.

1.3 Verwendeter Algorithmus

Um das Problem zu lösen verwende ich den rekursiven Backtracking Algorithmus.

Bei dem zu lösenden Problem muss man viele mögliche Wege ausprobieren. Dabei soll mit Hilfe eines festgelegten Musters ein Weg auf dem vorgegebenen Lösungsraum gewählt werden. Deswegen verwende ich den Backtracking Algorithmus.

Ähnliche Probleme sind das “finden eines Weges“, das “n – Damen Problem“ oder das “Rucksackproblem“, wobei entweder eine oder die beste Möglichkeit gesucht wird.

Weil in der Aufgabenstellung nur nach einer Lösung gefragt ist, kann der Algorithmus nach der ersten gefundenen Lösung mit der Suche aufhören.

Das Springerproblem, was in unserem Fall vorliegt, ist ein sehr bekanntes Problem, dessen Optimierungsmöglichkeiten bekannt sind. Mir war das genaue Problem noch nicht bekannt gewesen, weswegen ich den einfachen Backtracking Algorithmus gewählt habe, der nicht sehr effizient ist, aber die normale Vorgehensweise sehr gut verdeutlicht. Da ich am ersten Tag keine dieser Optimierungen kannte, habe ich meinen Algorithmus auch entsprechend aufgebaut und keine gefundenen Optimierungsmöglichkeiten übernommen, da dies in der Aufgabenstellung auch nicht gefordert war.

2 Verfahrensbeschreibung

2.1 Logische Datenstrukturen

2.1.1 Matrix

Diese Datenstruktur enthält als zentrales Element des Programms die Matrix. Durch die Kapselung der Matrix kann der Zugriff auf dieses Element genau kontrolliert werden. Alle Operationen, die von der Klasse Daten erhalten, sind als getter-Funktionen (get* + is*) implementiert. Dadurch wird gewährleistet, dass die von der Klasse benötigten Daten über feste Schnittstellen übergeben werden. Es gibt nur wenige setter-Funktionen (set*), die Schnittstellen zur Änderung der Matrix bereitstellen. Außerhalb des Pakets Verarbeitung, kann die Matrix initialisiert , der Startpunkt gesetzt und Sperrfelder können eingetragen werden. Alle setter-Funktionen werden Konsistenzprüfungen unterzogen, so dass es zu keinen korrupten Daten für den Programmablauf kommen kann. Zudem werden noch zwei weitere Schnittstellen innerhalb des Pakets Verarbeitung zur Verfügung gestellt, die vom Kernalgorithmus verwendet werden und direkteren Zugriff haben.

Name	Beschreibung	Datentyp
matrix	Zentrales Feld zur Speicherung der Daten	ganzzahliges zweidimensionales Feld
startpunkt	Koordinaten des Startpunktes	Datenstruktur Punkt
sperrFeldAnzahl	Anzahl der Sperrfelder in der Matrix	ganzzahlig
isInitialisiert	Speichert, ob die Matrix initialisiert wurde	Boolescher Typ
wegGefunden	Speichert, ob ein Sprungweg gefunden wurde	Boolescher Typ

Internen Werte des Feldes Matrix:

-1	Sperrfeld
0	besuchbar
>0	Wegnummerierung

Die Matrix wird intern mit den Indizes eines Feldes verwaltet, das heißt, dass die Nummerierung bei 0 und nicht bei 1 beginnt. Die Eingabedaten werden dementsprechend verarbeitet und auf das interne Format umgesetzt. Man findet die Bezeichnung meist in der Reihenfolge y-Koordinate und dann erst die x-Koordinate. Dies liegt an der internen zeilenweisen Speicherung der Daten, die erst in y-Richtung und dann erst in x-Richtung definiert ist. Eine weitere Besonderheit ist die Tatsache, dass sich der Nullpunkt in der linken oberen Ecke befindet und somit nicht wie ein normales Koordinatensystem aufgebaut ist. Den internen Aufbau der Matrix kann man an der unten folgenden Zeichnung (Abbildung 1) sehr gut erkennen:

Abbildung 1

2.1.2 Punkt

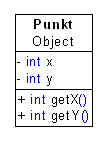Diese Datenstruktur speichert einen Punkt. Ein Punkt wird in der zwei dimensionalen Matrix durch eine y-Koordinate und eine x-Koordinate beschrieben. Dieser Datentyp wird direkt bei der Erstellung initialisiert und bietet Zugriff auf die beiden Koordinatenelemente.

Name	Beschreibung	Datentyp
x	x-Koordinate des Punktes	ganzzahlig
y	y-Koordinate des Punktes	ganzzahlig

2.2 Algorithmus

2.2.1 Gesamtverfahren

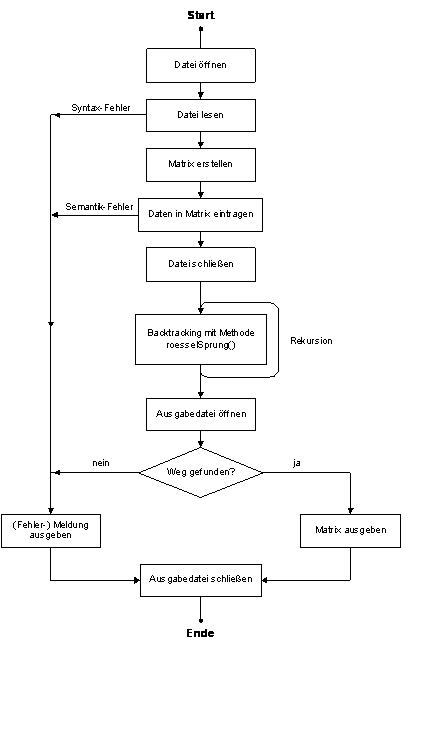
Abbildung 2

2.2.2 Eingabe

Die Kommentare werden zuerst aus dem Eingabestrom entfernt, dann erfolgt die eigentliche Eingabe.

Bei der Eingabe wird zuerst die Dimension der Matrix gelesen. Dann folgt das Einlesen des Startpunktes. Nachdem die Anzahl der Sperrfelder eingelesen ist, läuft eine Schleife so oft, bis alle Sperrfelder eingelesen sind. Sämtliche syntaktische Prüfungen sind direkt in der Eingabe vorhanden, wobei die semantischen Prüfungen erst in dem Objekt Matrix gemacht werden.

2.2.3 Hauptalgorithmus

Definition Backtracking:

Backtracking ist eine systematische Suchstrategie und findet deswegen immer eine optimale Lösung, wenn eine vorhanden ist. Dabei wird höchstens einmal in der gleichen "Sackgasse" gesucht. Backtracking ist sehr einfach über Rekursion zu programmieren, hat allerdings im schlechtesten Fall eine Laufzeit von O(8ⁿ), für dieses spezielle Problem.

Nun zu meinem Algorithmus:

Der Hauptalgorithmus ist die Suche nach einem Sprungweg mittels Rösselsprüngen über alle besuchbaren Felder. Um einen möglichen Weg zu finden, wird der klassische Backtracking -Algorithmus eingesetzt. Zuerst einmal muss man das Problem dazu in Teilprobleme zerlegen. Ein Teilproblem ist die Richtung des nächsten Sprungs zu bestimmen. Die 8 Sprungrichtungen kann man aus der folgenden Zeichnung entnehmen. Begonnen wird in Richtung Nordnordost und weitergesucht wird im Uhrzeigersinn. Dies entsprach der Reihenfolge aus dem Aufgabenbeispiel.

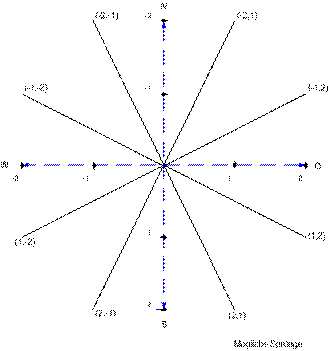
Abbildung 3

Bei der Rekursion überprüft die Funktion, ob sie gerade auf einem gültigen Feld steht. Ist dies nicht der Fall, so wird diese beendet und die Programmfolge geht in der Aufruffunktion weiter. Wenn die Funktion mit einem gültigen Funktionswert aufgerufen wurde, so trägt sie ihre Sprungnummer auf ihrer aktuellen Position in der Matrix ein. Die Sprungnummer entspricht der Rekursionstiefe und wird als Variable in den Funktionsaufrufen übergeben. Durch die bekannte Anzahl der besuchbaren Felder kann somit bestimmt werden, ob alle Felder besucht wurden. Wenn dies der Fall ist, kann der Algorithmus mit der Suche aufhören, da nur eine Möglichkeit ausgegeben werden soll. Die Rekursion kann dann mit wahr beendet werden. Ansonsten wird die Funktion weiter ausgeführt, wobei die Abarbeitung für diesen Teil der Rekursion abgeschlossen ist. Es folgt die Zerlegung in weitere Teilprobleme. Dazu ruft sich die Funktion selber mit den Koordinaten der acht Richtungen auf und überprüft die Ausgabewerte der Funktionen. Wird eine Rekursion erfolgreich beendet, so wird die aktuelle Funktion auch mit dem Wert wahr beendet. Sind alle acht Richtungen durchlaufen und es wurde bei den Funktionsaufrufen kein Sprungweg gefunden, so wird die aktuelle Position in der Matrix wieder als frei markiert und die Funktion wird mit dem Wert falsch beendet.

Es folgt ein Beispiel, an dem der Algorithmus näher erklärt wird:

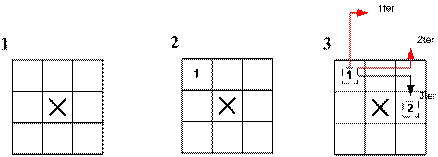
1. Schritt:

Die Matrix wird mit den Sperrfeldern initialisiert, hier das Feld (2,2)

2. Schritt:

Die Funktion roesselSprung() wird mit dem angegebenen Startwert (1,1) angesprungen. Da die Rekursionstiefe 1 ist, aber 8 ( m-Dimension * n-Dimension – Anzahl Sperrfelder) Felder besucht werden müssen, ist der Algorithmus weiter auszuführen.

3. Schritt:

Man fängt im Nordnordosten an, ein mögliches Sprungziel zu finden. Da man sich dort nicht mehr in der Matrix befindet, bricht dieser Funktionsaufruf ab und die nächste Position wird im Uhrzeigersinn überprüft. Dort befinden wir uns immer noch außerhalb der Matrix, weswegen die Suche weiter fortgesetzt wird. Der nächste Funktionsaufruf ist erfolgreich, da die Position (2,3) innerhalb der Matrix liegt und ein freies Feld ist, somit kann die Rekursion weitergeführt werden.

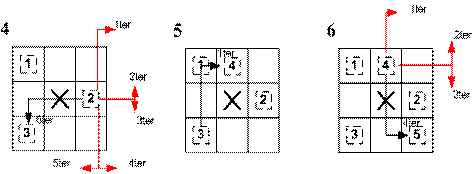
4. Schritt:

Bei diesem Schritt erkennen wir, dass die ersten fünf Sprungziele außerhalb der Matrix liegen und erst der 6. Sprung ein freies Feld liefert. Wir befinden uns in der Rekursionstiefe 3, dessen Wert auch in der Matrix vermerkt wird.

5. Schritt:

Hier suchen wir ein freies Feld an der Position (1,2), welches auch sofort gefunden und in der Matrix eingetragen wird. Ab hier erkennt man auch schon das zyklische Setzen der Werte in diesem Beispiel.

6. Schritt:

Die ersten drei Sprungziele liegen außerhalb der Matrix, wobei der 4. Schritt ein freies Feld findet.

7. Schritt:

Hier laufen sechs Sprungziele ins Leere, bevor die erste freie Position an der Stelle (2,1) gefunden wird. Die aktuelle Rekursionstiefe von mittlerweile 6 wird in das Feld geschrieben.

8. Schritt:

Es sind noch 2 Felder zu besuchen, wobei hier im zweiten Versuch ein freies Feld gefunden wird und nun im nächsten Schritt geschaut werden kann, ob das Rekursionsende erreicht ist.

9. Schritt:

Die ersten vier Sprungziele liegen außerhalb der Matrix und das 5. Sprungziel liefert ein freies Feld. Unsere vorher berechnete Rekursionstiefe von 8 ist erreicht und wir haben damit alle besuchbaren Felder genau einmal besucht und die Rekursion kann abgebrochen werden.

2.2.4 Ausgabe

Bei der Verarbeitung wird erkannt, ob eine Folge von Sprüngen durchgeführt werden konnte. Wurde ein Weg durch die Matrix gefunden, so wird die Matrix in einer doppelt geschachtelten Schleife ausgegeben. Wenn kein Weg entdeckt wurde, erscheint allein diese Meldung.

Neben der normalen Ausgabe gibt es noch eine Fehlerausgabe, die in einem Fehlerfall die nötigen Meldungen an den Benutzer zurückgibt. Dazu erkennt das Programm, welcher Fehler aufgetreten ist und gibt eine passende Meldung dazu aus.

2.3 Struktogramme

2.3.1 Eingabe

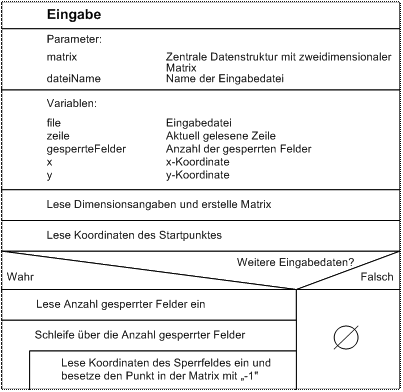
2.3.2 Verarbeitung

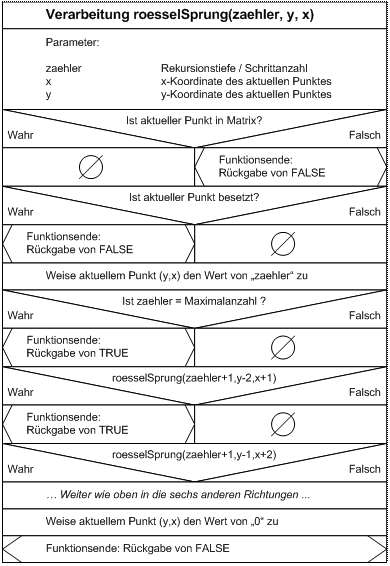
2.3.3 Ausgabe

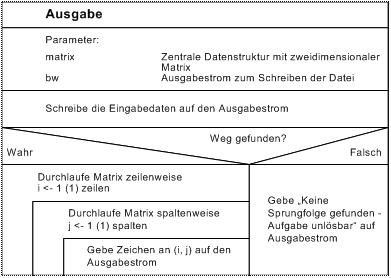
3 Programmbeschreibung

3.1 Paketbeschreibung

3.1.1 main

Diese Klasse steuert den Ablauf des Programms. Da hier auch zentral Fehler abgefangen werden, war es nötig, die Ausgabedatei schon sehr früh im Programmablauf zu öffnen, da Exceptions sonst nicht in die Ausgabedatei geschrieben werden könnten. In dieser Klasse befindet sich auch das zentrale Matrix-Element, welches per Referenz an die Module Eingabe, Verarbeitung und Ausgabe übergeben wird.

Zudem befindet sich hier der Parser für die Eingabeparameter. Dieser sorgt dafür, dass wichtige Flags in dieser Klasse gesetzt werden. Geparst werden:

-d DATEINAME (erkennt den Parameter und setzt den Dateinamen)
-debug (setzt das Programm in den Debugmodus, bei dem die Ausgaben auch auf dem Bildschirm ausgegeben werden).
-overwrite (überschreibt eine vorhandene Ausgabedatei. Dies erleichtert das Testen, kann aber im normalen Ablauf unerwünscht sein)
-h (zeigt die Hilfe an, wie das Programm aufgerufen wird. Die Hilfe wird auch automatisch angezeigt, wenn Parameter falsch angegeben wurden)

3.1.2 main.eingabe

Dieses Modul liest die Eingabedatei aus. Außerdem findet hier ein Teil der Syntaxüberprüfung statt, welcher die Eingabedaten auf Korrektheit überprüft.

3.1.3 main.verarbeitung

Im Modul Verarbeitung befinden sich zwei Hauptklassen:

Die Klasse Verarbeitung sucht einen Weg von Rösselsprüngen in der angegebenen Matrix. Dazu wird die Matrix übergeben, in der die einzelnen Schritte gespeichert werden.
Hier ist der Kernalgorithmus des Programms zu finden, der das Problem löst.

Die Klasse Matrix übernimmt die Verwaltung der Matrix. Dabei befindet sich die Matrix selber als zentrales Element in dieser Klasse. Alle Operationen, die die Matrix verändern, werden durch Setter zur Verfügung gestellt, die direkt Konsistenzprüfungen durchführen. Alle Operationen, die Daten aus der Matrix abfragen sind über Getter definiert, die die Daten aufbereitet zur Verfügung stellen.
Zudem gibt es noch Prüfungen, die auch direkt in dieser Klasse definiert sind und boolesche Ergebnisse zurückliefern. Die Schnittstellen dieser Klasse sind möglichst vielfältig, um alle nötigen Eingaben zu ermöglichen. Um die Übersichtlichkeit zu wahren, wurde hier ein Großteil der Funktionalität für die Matrix implementiert.

3.1.4 main.ausgabe

Im Paket Ausgabe befinden sich zwei Hauptklassen:

Die Klasse Ausgabe formatiert den Inhalt der Matrix für die grafische Ausgabe und gibt diese auf den angegebenen Ausgabestrom aus. Dabei wird sowohl die initiale Matrix, als auch die Matrix mit dem gesuchten Wert ausgegeben.

Die Klasse FehlerAusgabe dient zur Verarbeitung und Ausgabe von Fehlern. Dabei bekommt die Klasse ein Objekt des Typs Exception übergeben, welches dann genauer untersucht wird und eine hier definierte Meldung ausgibt.

3.1.5 main.tools

Das Modul Tools bietet Funktionalitäten, welche nicht anwendungsspezifisch sind und so auch in anderen Programmen benutzt werden können. Dazu zählt die Klasse MyLineNumberReader, welche den Kommentar und führende Leerzeichen aus dem Eingabestream entfernt.

Außerdem befindet sich die Klasse OutputFile in diesem Modul, welche aus dem Namen der Eingabedatei einen Writer auf die Ausgabedatei zurückgibt.

3.2 Modulplan

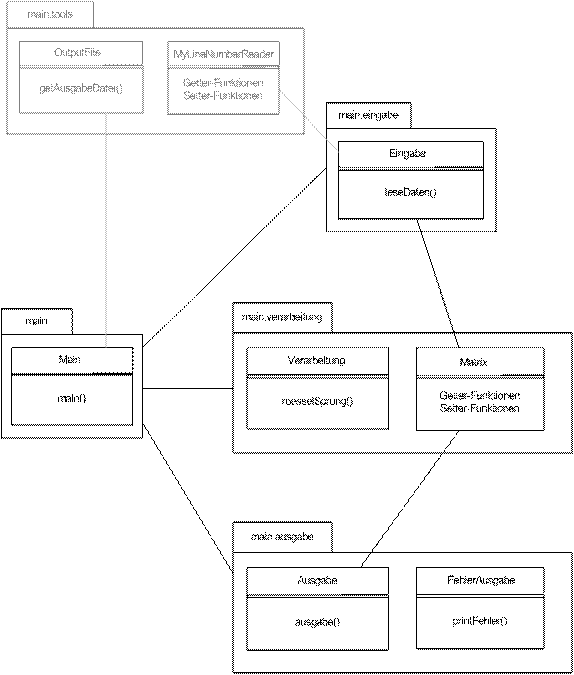
Abbildung 4

3.3 Schnittstellen

3.3.1 Eingabe

3.3.1.1 Eingabe

Die Eingabe liest die Daten von einer Eingabedatei, deren Name übergeben wurde, in die übergebene Instanz der Klasse Matrix.

public Eingabe( Matrix matrix,java.lang.String dateiName)

throws

UnexpectedCharacterException,

UnexpectedLineException,

UnknownCharacterException,

TooFewCharactersException,

TooFewSperrfelderException,

FileNotFoundException,

IOException,

IsSperrfeldException,

IsStartpunktException,

WrongDimensionException

Parameter:

matrix - Zentrale Datenstruktur mit Matrix

dateiName - Name der Eingabedatei

Ausnahmebehandlung:

UnexpectedCharacterException - Unerwartetes Zeichen

UnexpectedLineException - Unerwartete Zeile

UnknownCharacterException - Unbekanntes Zeichen

TooFewCharactersException – Zu wenig Zeichen angegeben

TooFewSperrfelderException – Zu wenig Sperrfelder angegeben

FileNotFoundException - Datei wurde nicht gefunden

IOException - Fehler bei der Eingabe

IsSperrfeldException - Doppeldefinition von Sperrfeld

IsStartpunktException - Sperrfeld auf Startfeld definiert

WrongDimensionException - Falsche Dimensionsangaben

3.3.2 Verarbeitung

3.3.2.1 Verarbeitung

Die Klasse Verarbeitung führt die Folge von Rösselsprüngen aus und schreibt einen gefundenen Weg in die übergebene Instanz der Klasse Matrix.

public Verarbeitung(Matrix matrix)

throws

MatrixNotInitialisedException

Parameter:

matrix - Zentrale Datenstruktur mit Matrix

Ausnahmebehandlung:

MatrixNotInitialisedException - Matrix nicht initialisiert

3.3.2.2 Matrix

Das zentrale Datenobjekt, welches mit seinen Schnittstellen Zugriffmöglichkeiten auf das zweidimensionale Feld bietet.

public Matrix()

void main.verarbeitung.Matrix.setMatrix (int m, int n)

throws

WrongDimensionException

Parameter:

m - y-Dimension der Matrix

n - x-Dimension der Matrix

Ausnahmebehandlung:

WrongDimensionException - Falsche Dimensionsangabe

void main.verarbeitung.Matrix.setSperrfeld (int y, int x)

throws

OutOfMatrixException

IsSperrfeldException,

IsStartPunktException,

Parameter:

y - y-Koordinate des Sperrfeldes

x - x-Koordinate des Sperrfeldes

Ausnahmebehandlung:

OutOfMatrixException - Sperrfeld außerhalb der Matrix

IsSperrfeldException - Sperrfeld schon vorhanden

IsStartpunktException - Sperrfeld auf Startpunkt

void main.verarbeitung.Matrix.setStartpunkt (int y, int x)

throws

OutOfMatrixException,

ReDefindesStartpunktException

Parameter:

y - y-Koordinate des Startpunktes

x - x-Koordinate des Startpunktes

Ausnahmebehandlung:

OutOfMatrixException - Startpunkt außerhalb der Matrix

ReDefinedStartpunktException - Mehrfacher Startpunkt

3.3.3 Ausgabe

Die Klasse Ausgabe schreibt eine gefundene Matrix formatiert auf die übergebene Ausgabedatei.

public Ausgabe(Matrix matrix, java.io.BufferedWriter bw)

throws

java.io.IOException

Parameters:

matrix - Zentrale Datenstruktur mit Matrix

bw - BufferedWriter der Ausgabedatei

Ausnahmebehandlung:

java.io.IOException - Ausgabedatei konnte nicht geschrieben werden

4 Benutzeranleitung

4.1 Benutzer des Gesamtsystems

4.1.1 Installation

Die Version des Programms wurde auf Windows 2000 Service Pack 4 erstellt. Durch den erzeugten Bytecode ist das Programm auf vielen Plattformen lauffähig. Um die folgenden Schritte auszuführen ist es nötig, die Verzeichnisse /Programm und /Test auf einem beschreibbaren Medium zu speichern.

Das ausführbare jar-Archiv programm.jar befindet sich auf der CD im Verzeichnis /Programm, dieses ist zur Ausführung des Programms gedacht. Der Bytecode befindet sich auf der CD im Ordner /Programm/bin, wobei der zugehörige Quellcode im Verzeichnis /Programm/src zu finden ist. Weitere Inhalte der CD können dem Inhaltsverzeichnis der CD entnommen werden, welches über die Datei index.html zu erreichen ist.

Das Programm kann mit dem Befehl:

javac main/Main.java

des Java Compilers javac übersetzt werden, wenn man sich im Verzeichnis /Programm befindet.

Alternativ kann man auch das Makefile mit dem Befehl make verwenden, welches im Verzeichnis /Programm/src ist. Dieses generiert auch das ausführbare jar-Archiv programm.jar, welches dann im Verzeichnis /Programm zu finden ist.

4.1.2 Programmaufruf

Das Programm wird über die Kommandozeile mit der Anweisung:

java –jar programm.jar –d <Eingabedatei>

gestartet. Es ist zudem möglich, die Ausgabe zusätzlich auf den Bildschirm umzulenken, indem man das Programm mit dem Befehl:

java –jar programm.jar –d <Eingabedatei> -debug

aufruft. Aus Sicherheitsgründen wird eine existierende Ausgabedatei defaultmäßig nicht überschrieben. Mit dem Befehl:

java –jar programm.jar –d <Eingabedatei> -overwrite

ist es allerdings auch möglich die Ausgabedatei zu überschreiben.

Bei falscher Parameter Eingabe, sowie bei Eingabe des Parameters -h bekommt man die Hilfe auf dem Bildschirm angezeigt. Alle Parameter können auch kombiniert werden.

Das Programm verarbeitet immer genau eine Eingabedatei und erzeugt eine Ausgabedatei mit der Endung ".out". Um eine Testreihe (Testsuite) durchzuführen gibt es mehrere Möglichkeiten. Eine Möglichkeit ist das Programm testautomation.jar welches im Verzeichnis /Test liegt. Es wird über den Aufruf

java –jar testautomation.jar

gestartet. Es erscheint eine graphische Oberfläche, bei der mit jedem Druck auf den Button "Start" ein Testlauf durchgeführt wird. Dabei werden eventuell vorhandene Ausgabedateien überschrieben. Um die Bedienung so einfach wie möglich zu gestalten, wurden die Pfade zum Programm an die Verzeichnisstruktur angepasst. Hier wurde bewusst ein Java Programm zur Testautomation verwendet, um eine Portierung auf mehrere Betriebssysteme zu ermöglichen.

Zudem findet sich auch ein Batchskript, sowie ein Shellskript im Verzeichnis /Test, welche auch eine Testreihe durchführen.

4.1.3 Spezifikation der Eingabedaten

Die Eingabedaten werden aus einer ASCII-Textdatei gelesen, welche dem Programm beim Aufruf als Parameter übergeben wird.

** Beispiel 1 : 1.Zeile Dimensionen m,n

** 2. zeile Koordinaten des Startfeldes 3. Anzahl gesperrter Felder

** 4. und Folgende Koordinaten dieser Felder

5 4

1 1

1 4

5 1

Die Eingabedatei kann Kommentare enthalten, welche mit einem doppeltem Stern (**) eingeleitet werden müssen. Dabei gilt die restliche Zeile als Kommentarzeile (vergleichbar mit Java Zeilen-End-Kommentaren).

Danach folgt die Angabe der y-Dimension und x-Dimension des Feldes, wobei hier nur Ganzzahlen im Bereich von 1-6 zugelassen sind.

In der nächsten Zeile erfolgt dann die Eingabe der y-Koordinate und x-Koordinate des Startpunktes, wobei dieser Punkt innerhalb der oben definierten Grenzen der Matrix liegen muss.

Dann erfolgt in der nächsten Zeile die Angabe der Anzahl der Sperrfelder, welche als Ganzzahl eingegeben wird.

In den darauf folgenden Zeilen werden die Sperrpunkte angegeben, wobei y-Koordinate und x-Koordinate als Ganzzahl innerhalb der Grenzen der Matrix einzutragen sind. Allerdings müssen genau soviel Sperrfelder angegeben werden, wie in der Anzahl definiert wurde.

4.1.4 Ausgabe des Programms

Das Programm gibt die Ausgabe direkt auf eine Ausgabedatei aus, die den Namen der Eingabedatei, sowie die Endung .out hat.

Bei der Ausgabe gibt es zwei verschiedene Arten. Auf der einen Seite gibt es die Ausgabe der Normal- und Sonderfälle, auf der anderen Seite gibt es die Ausgabe der Fehlerfälle.

Bei den Normal- und Sonderfällen gibt es zwei verschiedene Möglichkeiten, einen möglichen Weg und keinen gefundenen Weg. Gleich bei beiden Möglichkeiten ist, dass zuerst die Matrix im Eingabezustand ausgegeben wird, dann wird ein eventuell gefundener Weg ausgegeben (Testfall: Beispiel 1 aus der Aufgabenstellung) oder eine Meldung, dass kein Weg gefunden wurde (Testfall: Beispiel 2 aus der Aufgabenstellung.

Bei den Fehlerfällen erfolgt im Normalfall eine Ausgabe der Eingabedatei mit Zeilennummerierung, wenn dies möglich ist und danach folgt dann der passende Fehlertext (Testfälle: Fehlerfälle 1-6). Bei falschem Aufruf des Programms wird eine Meldung mit Art der falschen Eingabe, sowie eine Hilfe zum Aufruf des Programms ausgegeben.

4.1.5 Listing der Fehlermeldungen

Fehlermeldung	Behebung
Zuviel Eingaben in Zeile X	Überflüssige Zeichen aus der Zeile entfernen
Es folgen noch Zeichen nach der Eingabe in Zeile X	Überflüssige Zeilen mit Zeichen aus der Datei entfernen
Unbekanntes Zeichen in der Eingabe in Zeile X	Überprüfen, ob auch nur Ganzzahlen (außer Kommentar) in der Eingabe stehen
Zu wenig Zeichen für Eingabe in Zeile X	Die Daten hinzufügen, die für die Verarbeitung nötig sind
Es sind zu wenige Sperrfelder angegeben	Überprüfen, ob die Anzahl der Sperrfelder stimmt
Falsche Dimensionsangaben für Matrix	Die Dimensionsangaben der Matrix innerhalb der angegebenen Grenzen definieren
Startpunkt S(x,y)/Sperrfeld X(x,y) außerhalb der Matrix definiert	Den angegeben Punkt anpassen, so dass er innerhalb der Matrix liegt
Sperrfeld auf Startpunkt (x,y) definiert	Das Sperrfeld muss unterschiedliche Koordinaten, wie das Startfeld haben
Sperrfeld (x,y) doppelt definiert	Ein Sperrfeld soll nur einmal in der Eingabe vorkommen
Die Eingabedatei wurde nicht gefunden	Namen und Pfad der Eingabedatei richtig angeben
Die Datei DATEINAME existiert schon	Entweder muss die vorhandene Ausgabedatei gelöscht werden oder das Programm wird mit dem Parameter "-overwrite" aufgerufen
Es wurde kein Parameter für das Programm übergeben.	Es müssen beim Aufruf des Programms Parameter angegeben werden
Es ist ein Fehler bei der Ausgabe aufgetreten	Beim Schreiben auf den Ausgabestrom ist ein Fehler geschehen. Die Systemressourcen können aufgebraucht sein.
Die Ausgabedatei konnte nicht beschrieben werden	Die Ausgabedatei oder das Dateisystem müssen beschreibbar sein

4.2 Benutzer des Unterprogramms mit dem Lösungsalgorithmus

Das Unterprogramm befindet sich in dem Paket main.verarbeitung. Durch die strikte Trennung von Eingabe, Verarbeitung und Ausgabe (EVA-Prinzip) ist es möglich, das Paket unabhängig von dem Rest des Programms zu verwenden.

4.2.1 Syntax des Unterprogrammaufrufs

Bevor die Klasse Verarbeitung aufgerufen werden kann, muss ein Objekt der Klasse Matrix, welche im gleichen Paket liegt, erzeugt und dann initialisiert werden. Dazu erstellt man eine Instanz der Klasse und ruft die Funktion setMatrix(int, int) mit den Dimensionsangaben auf. Dann muss noch ein Startpunkt mit den Koordinaten über setStartpunkt(int, int) erstellt werden. Wenn Sperrfelder angegeben werden sollen, so können diese über die Methode setSperrfeld(int, int) gesetzt werden. Um dann eine Sprungfolge zu finden, wird der Konstruktor der Verarbeitung aufgerufen. Das Ergebnis findet sich nun in der Instanz der Klasse Matrix wieder und kann mit entsprechenden Gettern abgefragt werden.

Folgender Ablauf zeigt dies genauer:

Matrix matrix = new Matrix();

matrix.setMatrix(m,n);

matrix.setStartpunkt(y,x);

[matrix.setSperrfeld(y,x);]

new Verarbeitung(matrix);

4.2.2 Übergabeparameter

public void setMatrix (int m, int n) throws WrongDimensionException

public void setStartpunkt (int y, int x) throws OutOfMatrixException, ReDefinedStartpunktException

public void setSperrfeld (int y, int x)

throws

OutOfMatrixException,

IsSperrfeldException,

IsStartpunktException

public Verarbeitung(Main matrix) throws MatrixNotInitialisedException

4.2.3 Plausibilitätsprüfungen

Um die oben genannten Funktionalitäten zu benutzen, müssen entsprechende Konstrukte verwendet werden, die die Exceptions auffangen können. Fehlermeldungen werden nicht vom Algorithmus ausgegeben, allerdings ist durch das Werfen der Exceptions gewährleistet, dass sämtliche semantischen Fehler der Bedienung erkannt und weitergegeben werden können. Eine genaue Beschreibung der Schnittstellen ist auf der CD in dem von Javadoc bzw. Doxygen generierten Output in HTML Form zu finden.

5 Entwicklungsumgebung

5.1 Rechner und Betriebssystem

Der Rechner ist ein Hewlett Packard Vectra Rechner, der über einen Arbeitsspeicher von 256MB und eine Festplattenkapazität von 30GB verfügt.

Als Betriebssystem läuft Windows 2000 in der Version 5.00.2195 mit Service Pack 4.

Zudem wurde ein weiterer Rechner gleicher Bauart mit dem Betriebssystem Suse Linux 8.2 als CVS Server eingesetzt.

5.2 Vernetzung und Peripherie

Das Programm wurde auf einem Client eines heterogenen Netzes geschrieben. Zur Zeit sind ca. 800 Personal Computer als Arbeitsstationen im Netz integriert. Sie alle können über verschiedene „Print-Server“ auf mehrere postscriptfähige Laserdrucker zugreifen. Des Weiteren bietet das Netzwerk den Zugriff auf mehrere Terabyte Plattenkapazität, welche von einem SAN (Storage Area Network) verwaltet werden. Die Daten werden über das Netzwerk von mehreren Backup-Robotern gesichert.

5.3 Programmiersprache und Compiler

Zur Implementierung habe ich die Programmiersprache Java gewählt. Die Gründe sind:

Ein sehr wichtiges Merkmal von Java ist die Plattformunabhängigkeit der übersetzten Programme. Einmal übersetzte Java-Programme (sogenanter Java Byte-code) sind auf jeder Rechnerplattform ausführbar, die über eine geeignete Java-Laufzeitumgebung (Java Virtual Machine) verfügt.

Java ist voll objekt-orientiert und muss keine Kompatibilitäten zu älteren Programmiersprachen (C -> C++) enthalten
Java bietet mir eine sehr effektive Implementierungsmöglichkeit in der Sprache selbst, sowie in weiteren Paketen, die zu Java gehören
gute Entwicklungsumgebungen für effektives Programmieren (Bsp.: Eclipse)
zudem ist Java sehr gut dokumentiert (Java API über javadoc, sowie weite Verbreitung im Internet, da Java Applets auch ein Teil dieses sind)

Als Compiler zum Entwickeln und Testen verwendete ich das Java(TM) 2 SDK in der

Standard Edition Version 1.4.2 unter Windows 2000. Es implementiert die elementaren

Datentypen mit den nachfolgend aufgelisteten Wertebereichen. Die für Fließkommazahlen angegebenen Wertebereiche beziehen sich dabei nur auf deren absolute Beträge, die

gleichen Werte können auch im negativen Zahlenbereich angenommen werden.

Typgruppe	Typ	Speicher	Minimum	Maximum
Ganzzahl	byte	8 Bit	-128	127
	short	16 Bit	-32768	32767
	int	32 Bit	-2^-31	2³¹-1
	long	64 Bit	-2⁶³	2⁶³-1
Gleitkomma	float	32 Bit	10^-46	10³⁸(6 sign. Stellen)
	double	64 Bit	10^-324	10³⁰⁸ (15 sign. Stellen)

5.4 Hilfsmittel

Bei der Programmierung wurde als Entwicklungsumgebung Eclipse in der Version 2.1.2 verwendet
Bei der Dokumentierung wurde Word aus dem Office XP Paket verwendet
Zur Versionsverwaltung wurde CVS eingesetzt

6 Test

6.1 Test-Ablauf

6.1.1 Integrationstests

Das Programm wurde im Top-Down Ansatz entworfen. Hier geht man bei der Entwicklung so vor, dass man von Anfang an ein komplettes (lauffähiges) Programm hat und noch nicht implementierte Funktionalitäten als Leerfunktionen (Stubs) eingebunden sind. Vorteile sind, dass die Schnittstellen von Anfang an getestet werden und Fehler gut lokalisierbar sind. Allerdings verlangen die Stubs nach zusätzlichem Programmieraufwand, der aber durch die Vorteile aufgewogen wird.

6.1.2 Modultests

Die Modultests habe ich in Black-Box Tests und White-Box Tests aufgeteilt. Dazu habe ich einen Test-Baum erstellt, über den man die Testbeispiele systematisch erstellen kann. Durch meine Kenntnis des Quellcodes als Programmierer, habe ich schon bei der Programmierung White-Box Tests durchgeführt und versucht eine möglichst große Pfadüberdeckung zu erhalten. Einige dieser Tests sind auch in die Testbeispiele mit aufgenommen wurden. Bei den Black-Box Tests habe ich versucht vom Quellcode Abstand zu halten und die Testfälle in Klassen aufzuteilen.

6.1.3 Regressionstests

Genauso wie den Quelltext, verwalte ich meine Testbeispiele mit dem CVS. So kann ich zu jeder Version meines Programms einen Testdurchlauf machen, der dann im CVS gespeichert wird. Dadurch habe ich den Überblick, wo sich Änderungen in den Testbeispielen zwischen den Versionen ergeben haben. Nebeneffekte können schneller entdeckt werden und man kann genauer lokalisieren, zwischen welchen Versionen Fehler beseitigt wurden oder entstanden sind.

6.2 Testbeispiele

Zur Entwicklung der Testfälle wurde folgender Testbaum verwendet:

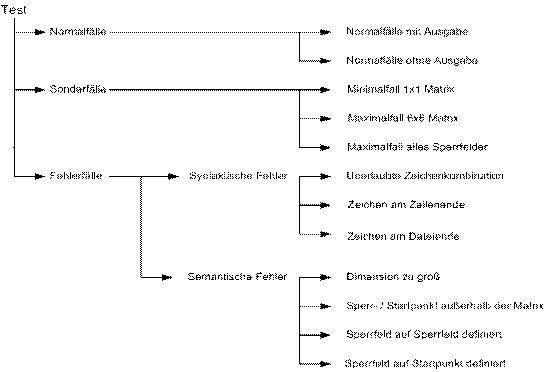
Abbildung 5

6.2.1 Testbeispiele aus der Aufgabenstellung

6.2.1.1 Beispiel 1

Eingabedaten:

*************

+ -- + -- + -- + -- +

| 1 | | | X |

+ -- + -- + -- + -- +

| | | | |

+ -- + -- + -- + -- +

| | | | |

+ -- + -- + -- + -- +

| | | | |

+ -- + -- + -- + -- +

| X | | | |

+ -- + -- + -- + -- +

Ausgabedatei:

*************

+ -- + -- + -- + -- +

| 1 | 14 | 17 | X |

+ -- + -- + -- + -- +

| 18 | 11 | 2 | 15 |

+ -- + -- + -- + -- +

| 13 | 16 | 5 | 8 |

+ -- + -- + -- + -- +

| 10 | 7 | 12 | 3 |

+ -- + -- + -- + -- +

| X | 4 | 9 | 6 |

+ -- + -- + -- + -- +

Das erste Beispiel stellt einen gewöhnlichen Normalfall dar, bei dem korrekte Eingangsdaten angegeben wurden, aus denen die Startmatrix erstellt werden konnte. In der Verarbeitung wird dann über Backtracking eine Sprungfolge gesucht. Der Algorithmus wurde in der Abarbeitungsreihenfolge an die Beispiele aus der Aufgabenstellung angepasst, somit konnte man ein richtiges Arbeiten des Algorithmus mit dem oberen Beispiel überprüfen. In dem Beispiel kommt auch die Tiefensuche zum Einsatz (Bsp.: Sprung von 12 auf 13), womit durch diesen Testfall fast der komplette Algorithmus getestet wird.

6.2.1.2 Beispiel 2

Eingabedaten:

*************

+ -- + -- + -- +

| 1 | | |

+ -- + -- + -- +

| | | |

+ -- + -- + -- +

| | | |

+ -- + -- + -- +

Keine Sprungfolge gefunden - Aufgabe unlösbar

Das zweite Beispiel steht für einen typischen Normalfall, bei dem keine Sprungfolge gefunden werden kann. Das mittlere Feld kann durch Rösselsprünge nicht erreicht werden (Schrittweite 2 überspringt das mittlere Feld) und somit terminiert der Algorithmus mit der obigen Meldung.

6.2.1.3 Beispiel 3

Eingabedaten:

*************

+ -- + -- + -- +

| 1 | | |

+ -- + -- + -- +

| | X | |

+ -- + -- + -- +

| | | |

+ -- + -- + -- +

Ausgabedatei:

*************

+ -- + -- + -- +

| 1 | 4 | 7 |

+ -- + -- + -- +

| 6 | X | 2 |

+ -- + -- + -- +

| 3 | 8 | 5 |

+ -- + -- + -- +

Das dritte Beispiel stellt einen Normalfall dar, bei dem es nicht zum eigentlichen Backtracking, wohl aber zu einer kompletten Abarbeitung der Sprungfolge kommt. Der erste Weg der komplett durchgegangen werden kann, ist auch direkt das Endergebnis. Genauer diskutiert wurde der Testfall unter 2.2.3 (Hauptalgorithmus), wo der Algorithmus in allen Schritten erklärt wird.

6.2.2 Normalfälle

6.2.2.1 Normalfall 1

Eingabedaten:

*************

+ -- + -- + -- + -- + -- +

| X | | | | |

+ -- + -- + -- + -- + -- +

| 1 | | | | |

+ -- + -- + -- + -- + -- +

| X | | | | |

+ -- + -- + -- + -- + -- +

| X | | | | |

+ -- + -- + -- + -- + -- +

| | | | | |

+ -- + -- + -- + -- + -- +

Ausgabedatei:

*************

+ -- + -- + -- + -- + -- +

| X | 7 | 2 | 21 | 16 |

+ -- + -- + -- + -- + -- +

| 1 | 22 | 17 | 8 | 3 |

+ -- + -- + -- + -- + -- +

| X | 11 | 6 | 15 | 20 |

+ -- + -- + -- + -- + -- +

| X | 18 | 13 | 4 | 9 |

+ -- + -- + -- + -- + -- +

| 12 | 5 | 10 | 19 | 14 |

+ -- + -- + -- + -- + -- +

Um das Programm im normalen Betrieb zu testen habe ich folgendes Beispiel ausgewählt, weil man am Endergebnis gut erkennen kann, dass eine gewissen Komplexität vorhanden ist und Backtracking zum Einsatz kommt. Verfolgt man die Sprungfolge vom Startpunkt aus, erkennt man, dass der Ablauf bis zum 6. Sprung genau mit der Aufruffolge im Uhrzeigersinn begonnen bei Nordnordost übereinstimmt. Dann erwarten wir die 7 dort, wo Position 21 steht. Daher wissen wir, dass das Backtracking auch nötig war. Die Richtigkeit des Beispiels erkennt man an dem Nachvollziehen der Sprungreihenfolge bis zum 22. Element. Somit lief ein größeres Beispiel richtig durch den Algorithmus.

6.2.2.2 Normalfall 2

Eingabedaten:

*************

+ -- + -- + -- + -- + -- + -- +

| 1 | | | | | |

+ -- + -- + -- + -- + -- + -- +

| | X | | | | |

+ -- + -- + -- + -- + -- + -- +

| | | | | | |

+ -- + -- + -- + -- + -- + -- +

| | | | | | |

+ -- + -- + -- + -- + -- + -- +

| | | | | X | |

+ -- + -- + -- + -- + -- + -- +

Keine Sprungfolge gefunden - Aufgabe unlösbar

Durch viele Normaltests konnte ich davon ausgehen, dass der Algorithmus richtig ist. Der Normalfall 2 wurde ausgewählt, weil dies eine recht große Matrix 5x6 mit keiner Lösung ist. Somit gibt 27 (5x6-3 Felder der Matrix – Startpunkt - Sperrfelder) Felder und somit sind 8²⁷ Prüfungen notwendig, um dies festzustellen (8 Richtungen mit der Rekursionstiefe 27). Das Beispiel hat eine Laufzeit von wenigen Sekunden und repräsentiert einen Normalfall der keine Sprungfolge findet. Das Programm terminiert mit der richtigen Ausgabe, dass keine Sprungfolge möglich ist, und gibt vorher die Eingangsmatrix aus.

6.2.3 Sonderfälle/Grenzfälle

6.2.3.1 Sonderfall 1

Eingabedaten:

*************

+ -- + -- + -- + -- + -- + -- +

| 1 | | | | | |

+ -- + -- + -- + -- + -- + -- +

| | | | | | |

+ -- + -- + -- + -- + -- + -- +

| | | | | | |

+ -- + -- + -- + -- + -- + -- +

| | | | | | |

+ -- + -- + -- + -- + -- + -- +

| | | | | | |

+ -- + -- + -- + -- + -- + -- +

| | | | | | |

+ -- + -- + -- + -- + -- + -- +

Ausgabedatei:

*************

+ -- + -- + -- + -- + -- + -- +

| 1 | 28 | 33 | 20 | 3 | 26 |

+ -- + -- + -- + -- + -- + -- +

| 34 | 19 | 2 | 27 | 8 | 13 |

+ -- + -- + -- + -- + -- + -- +

| 29 | 32 | 21 | 12 | 25 | 4 |

+ -- + -- + -- + -- + -- + -- +

| 18 | 35 | 30 | 7 | 14 | 9 |

+ -- + -- + -- + -- + -- + -- +

| 31 | 22 | 11 | 16 | 5 | 24 |

+ -- + -- + -- + -- + -- + -- +

| 36 | 17 | 6 | 23 | 10 | 15 |

+ -- + -- + -- + -- + -- + -- +

Der Sonderfall 1 behandelt den vorkommenden Maximalfall mit einer 6x6 Matrix. Mit dem Maximalfall können die Grenzen des Programms gut getestet werden. Es zeigt erst einmal, dass die Eingabeprüfung richtig funktioniert und die Eingaben als korrekt angenommen werden. Dies spiegelt sich auch in der, als Eingabedaten, erzeugten Matrix wieder. Des Weiteren sehen wir darunter eine mögliche Sprungreihenfolge. Dies zeigt, dass auch der Abbruch der Rekursion ordnungsgemäß funktioniert. Bei genauerer Betrachtung des Testfalls sieht man auch an diesem Beispiel das Eintreten des Backtracking (von Element 16 auf 17). Da es ein großes Beispiel ist, erkennt man auch, dass die Formatierung der Ausgabedaten und die Ausrichtung der Zahlen auch bei dem größten Fall komplett richtig ist.

6.2.3.2 Sonderfall 2

Eingabedaten:

*************

+ -- +

| 1 |

+ -- +

Ausgabedatei:

*************

+ -- +

| 1 |

+ -- +

Der zweite Sonderfall ist das Minimalbeispiel. Zuerst erkennt man wieder die richtige Prüfung der Eingabedaten, die eine 1x1 Matrix mit dem Startpunkt auf diesem Feld definiert. Bei der Ausgabe erkennt man, dass das Beispiel eine Sprungfolge findet, nämlich diese auf den Startpunkt. Jedes Feld wurde genau einmal besucht und das Beispiel wird in meinem Algorithmus als richtig angesehen.

6.2.3.3 Sonderfall 3

Eingabedaten:

*************

+ -- + -- + -- +

| X | X | 1 |

+ -- + -- + -- +

| X | X | X |

+ -- + -- + -- +

| X | X | X |

+ -- + -- + -- +

Ausgabedatei:

*************

+ -- + -- + -- +

| X | X | 1 |

+ -- + -- + -- +

| X | X | X |

+ -- + -- + -- +

| X | X | X |

+ -- + -- + -- +

Als letzten Sonderfall habe ich mir eine Matrix ausgesucht, die bis auf den Startpunkt mit Sperrfeldern besetzt ist. Zu erwähnen ist hier noch das Setzen des Startpunktes auf den Punkt, der sich genau an der linken oberen Ecke befindet. Somit ist auch dieser Fall überprüft, dass sich der Startpunkt an Maximal-/Minimalgrenzen der Matrix bewegt. Die restlichen Sperrfelder werden durch die Eingabe richtig abgearbeitet und bedecken alle anderen Felder, bis auf den Startpunkt. Die Eingabedaten sind somit komplett korrekt und der Algorithmus kann ausgeführt werden. Allerdings ist das einzig besuchbare Feld der Startpunkt, welcher angesprungen wird und somit jedes freie Feld genau einmal besucht ist. Der Algorithmus terminiert somit richtig und liefert als Ausgabe die Eingabematrix zurück.

6.2.4 Fehlerfälle

Erst einmal folgt eine Erklärung zum Aufbau der Ausgabe der Fehlerfälle. Tritt ein Fehlerfall auf, so wird die Eingabedatei mit Zeilennummern ausgegeben. Danach folgt die auf den Fehler passende Fehlermeldung mit einer Lokalisierung des Fehlers. Da viele Fehler einen Bezug zur Zeile haben, kann man durch die Fehlermeldung mit Zeilenbezug den Fehler in den Eingabedaten auch sofort anhand der Zeilennummerierung nachvollziehen und fehlerhafte Eingabedaten schnell korrigieren.

6.2.4.1 Fehlerfall 1

Eingabedaten:

*************

1: ** Fehlerfall 01

2: // Falsches Kommentarzeichen verwendet

3: 3 3

4: 1 1

5: 1

6: 2 3

Unbekanntes Zeichen in der Eingabe in Zeile 2

Dieser Fehlerfall testet eine fehlerhafte Kommentierung in der Eingabedatei. Die erste Zeile wird als Kommentar richtig verarbeitet, wobei in der zweiten ein falsches Kommentarzeichen verwendet wird, was einen syntaktischen Fehler darstellt. In der Eingabe wird festgestellt, dass dort ein Fehler im Format der Eingabedaten vorliegt. Also wird die Eingabedatei mit Zeilennummerierung ausgegeben. Der Fehler wird richtig als unbekanntes Zeichen erkannt, und die Zeilennummer 2 passt auch mit dem falschen Kommentar in der zweiten Zeile der Eingabedatei zusammen.

6.2.4.2 Fehlerfall 2

Eingabedaten:

*************

1: ** Fehlerfall 02

2: ** Unerlaubte Zeichenkombination in der Dimensionsangabe

3: 3 vier

4: 1 1

5: 1

6: 3 4

Unbekanntes Zeichen in der Eingabe in Zeile 3

Der zweite Fehlerfall beschreibt eine syntaktisch falsche Eingabedatei, bei der die x-Dimension der Matrix in wörtlicher Form und nicht als Zahl aufgeschrieben wurde. Laut Spezifikation sind aber nur ganzzahlige Werte als Dimensionsangaben erlaubt. Bei der Ausgabe wird die Eingabedatei mit Nummerierung richtig ausgegeben und der syntaktische Fehler wird richtig in der dritten Zeile gefunden. Somit kann auch die Behandlung des zweiten Fehlerfalls als richtig betrachtet werden.

6.2.4.3 Fehlerfall 3

Eingabedaten:

*************

1: ** Fehlerfall 03

2: ** Zeichen am Dateiende

3: 3 3

4: 1 1

5: 1

6: 2 3

7: 2 2

Es folgen noch Zeichen nach der Eingabe in Zeile 7

Mit dem dritten Fehlerfall wird getestet, ob semantisch fehlerhafte Eingaben bei der Sperrfeldanzahl erkannt werden. Im gewählten Fehlerfall wird die Sperrfeldanzahl mit 1 angegeben, wobei 2 Sperrfelder danach folgen. Da nicht klar ist, ob nur das erste Sperrfeld verarbeitet werden soll oder ob folgende Daten doch von Relevanz sind, wird hier ein Fehler ausgegeben, dass noch Daten nach den eigentlichen Programmdaten folgen. Es wird in dem Beispiel richtig erkannt, dass nur ein Sperrfeld verarbeitet werden soll, aber nach dem ersten Sperrfeld noch Daten in Zeile 7 folgen. Somit können unbeabsichtigte Fehleingaben bei der Sperrfeldanzahl zu keinen, für den Benutzer, falsch scheinenden Ausgaben folgen.

6.2.4.4 Fehlerfall 4

Eingabedaten:

*************

1: ** Fehlerfall 04

2: ** Dimensionen zu gross gewaehlt

3: 7 6

4: 3 2

5: 2

6: 1 1

7: 3 3

Falsche Dimensionsangaben für Matrix

Die maximale Dimension der Matrix ist sowohl in x-Richtung, als auch in y-Richtung mit der Größe 6 begrenzt und mit 1 als kleinstmöglicher Dimension definiert. Die Grenzen sind durch eine Konstante im Programm zu ändern, so dass auch weitere Maximaltests erfolgen können. Im vorliegenden Fehlerfall ist aber eine Dimension von der Größe in der Eingabedatei angegeben, womit die Grenzen aus der Aufgabenstellung überschritten sind. Dies stellt einen semantischen Fehler dar, der vom Programm erkannt werden sollte. In der Ausgabe sehen wir, dass der Fehler erkannt, die Eingabedatei ausgegeben wird und eine Fehlermeldung erfolgt, die zu dem Fehler passt, und ihn lokalisierbar macht.

6.2.4.5 Fehlerfall 5

Eingabedaten:

*************

1: ** Fehlerfall 05

2: ** Startpunkt ausserhalb der Matrix

3: 5 4

4: 6 3

Startpunkt S(6,3) außerhalb der Matrix definiert

Im fünften Fehlerfall wird die Matrix richtig definiert, allerdings befindet sich der gesetzte Startpunkt außerhalb der Matrix. Da dies für den Algorithmus einen Fehler darstellt, wird die Verarbeitung nicht ausgeführt und der Fehler bei der Definition des Startpunktes erkannt. Bei der Ausgabe erfolgt die Ausgabe der Eingabedatei, sowie eine präzise Fehlermeldung, die aussagt, dass der Startpunkt mit den Koordinaten y=6 und x=3 außerhalb der Matrix definiert ist. Vergleichen wir dies mit den Eingabedaten stellen wir fest, dass der Fehler richtig gefunden wurde, und durch die Angabe der Koordinaten ist der Fehler leicht zu beseitigen.

6.2.4.6 Fehlerfall 6

Eingabedaten:

*************

1: ** Fehlerfall 06

2: ** Sperrfeld auf Startpunkt

3: 5 5

4: 3 3

5: 1

6: 3 3

Sperrfeld auf Startpunkt(3,3) definiert

Im Folgenden Fehlerfall sind sowohl die Matrix, als auch der Startpunkt und die Anzahl der Sperrfelder richtig angegeben. Das Sperrfeld liegt auch innerhalb der Matrix, allerdings auf dem angegebenen Startpunkt. Ein Startpunkt ist für die Verarbeitung notwendig, somit kann dieser nicht überschrieben werden. Genauso fehlerhaft interpretiere ich eine doppelte Definition von Sperrfeldern, da von Fehleingaben seitens des Benutzers auszugehen ist, die zu unerwarteten Ergebnissen führen können. In diesem Fall sind sowohl der Startpunkt, als auch das Sperrfeld auf der Position y=3 und x=3 angegeben. Der Fehler in den Eingabedaten wird richtig erkannt und es erfolgt die Ausgabe, dass ein Sperrfeld auf dem Startpunkt mit der Position y=3 und x=3 definiert wurde.

6.2.5 Anmerkungen zu den Tests

Außer den hier beigefügten Integrationstests wurden noch weitere Testreihen durchgeführt, um eventuelle Schwachstellen im Programm aufzudecken.

Zudem wurden weitere Testreihen für den Parser der Eingabeparameter durchgeführt, die nicht mit in die Dokumentation aufgenommen wurden.